 |
| 3 y 4 y 5... sacos unidos 5 unidos sacos |
 | |
| trip on_by trip |
La banda de Möbius posee las siguientes propiedades:
- Tiene sólo una cara:
- Tiene sólo un borde:
- Esta superficie no es orientable:
- Otras propiedades:
Si se corta una cinta de Möbius a lo largo, a diferencia de una cinta normal, no se obtienen dos bandas, sino una banda más larga pero con dos vueltas. Si a ésta banda se la vuelve a cortar a lo largo, se obtienen otras dos bandas entrelazadas pero con vueltas. A medida que se van cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.[1]
Este objeto se utiliza frecuentemente como ejemplo en topología.
Topológicamente, la banda de Möbius puede definirse como el cuadrado ![\scriptstyle[0,1] \times [0,1]](http://upload.wikimedia.org/math/7/3/e/73e80ab91ce1e439d855abdc829e3c8e.png) que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación
que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación 
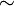
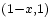 para
para  , como en el diagrama que se muestra en la figura de la derecha.
, como en el diagrama que se muestra en la figura de la derecha.
![\scriptstyle[0,1] \times [0,1]](http://upload.wikimedia.org/math/7/3/e/73e80ab91ce1e439d855abdc829e3c8e.png) que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación
que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación 
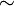
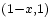 para
para  , como en el diagrama que se muestra en la figura de la derecha.
, como en el diagrama que se muestra en la figura de la derecha. La banda de Möbius es una variedad bidimensional (es decir, una superficie). Es un ejemplo estándar de una superficie no orientable. La banda de Möbius es un ejemplo elemental -también- para ilustrar el concepto matemático de fibrado topológico.
Precisamente, como objeto topológico, la banda de Möbius también es considerada como el espacio total  de un fibrado no trivial teniendo como base la 1-esfera
de un fibrado no trivial teniendo como base la 1-esfera 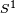 y fibra un intervalo, i.e.
y fibra un intervalo, i.e.
 de un fibrado no trivial teniendo como base la 1-esfera
de un fibrado no trivial teniendo como base la 1-esfera 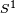 y fibra un intervalo, i.e.
y fibra un intervalo, i.e.
No hay comentarios:
Publicar un comentario